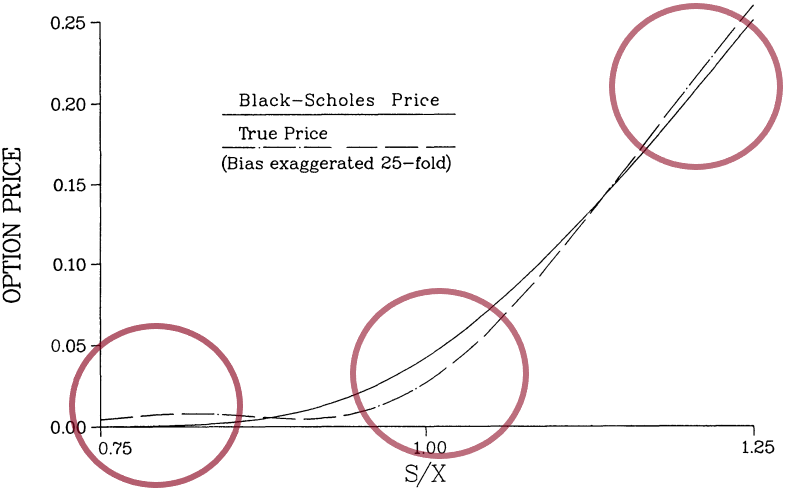
Due to its simplicity, the Black-Scholes-Merton (BSM) model has been widely used by financial institutions and traders for option pricing. However, the BSM model has a number of important assumptions that do not exist in the real world, and one of them is constant volatility. On a real market, volatility is a random, stochastic substance. One of the earliest attempts to improve the BSM by implementing stochastic volatility was the work by John Hull and Alan White, published in 1987 — The Pricing of Options on Assets with Stochastic Volatilities. The Hull-White stochastic-volatility model is useful to know and simple to implement, so, let's analyze it.

There are several regions with incredibly tense and unstable political situations and high anti-American sentiment. The probability of escalation in some of those regions is relatively high, and there is possibility of terrorist attacks on American companies. Starbucks is known as a supporter of the U.S. Military (Starbucks Stories, 2005) and an iconic American brand, so it could become one of the targets. In the following paragraphs, the hypothetical terrorist attack’s impact on Starbucks’ performance (immediate and 12-month effect) will be analysed.
The Global Financial Crisis was a unique phenomenon that not only affected many millions of people and tens of thousands of companies at the time but also impacted the global financial system and the future of financial institutions and services they provide. In order to better understand the issues, and to avoid repeating the same situations in the future (or, at least, mitigate the consequences), it is always important to learn the root causes. In the following paragraphs, the most important aspects of the crisis will be reviewed from the risk perspective: what gaps in risk assessment caused the crisis, what has improved in risk-management approaches since then, and how shocks change the financial-service landscape.
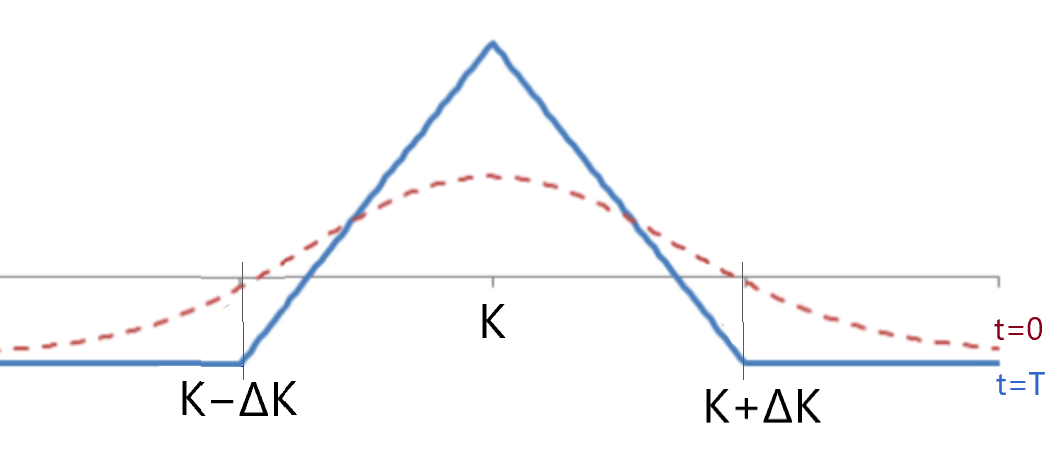
In a case when there are no orders in a DOM for a strike but there is necessary data for the lower and higher strikes, one of the ways to calc the find "fair" implied volatility (IV) (and hence, an option price) for the strike is to use Butterfly no-arbitrage condition. Let's see how to prove the absence of arbitrage and an example of the Butterfly equation use.
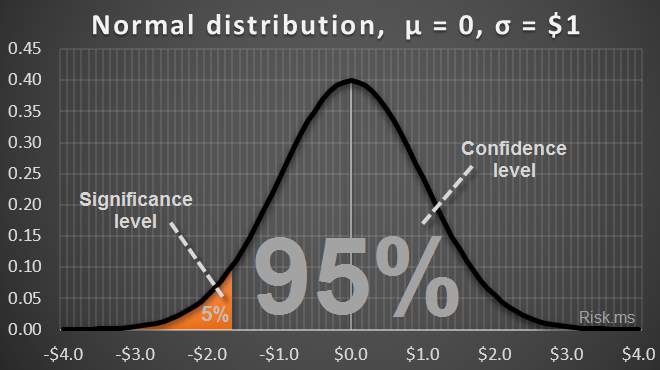
What is VaR
Value at Risk (VaR) is a measure of the market risk of loss for investments. VaR is a measure and it quantifies the level of financial risk (possible loss) within a firm or investment portfolio over a specific time frame with a pre-specified probability. VaR identifies the probability that losses will be greater than a pre-specified threshold.