What is VaR
Value at Risk (VaR) is a measure of the market risk of loss for investments. VaR is a measure and it quantifies the level of financial risk (possible loss) within a firm or investment portfolio over a specific time frame with a pre-specified probability. VaR identifies the probability that losses will be greater than a pre-specified threshold.
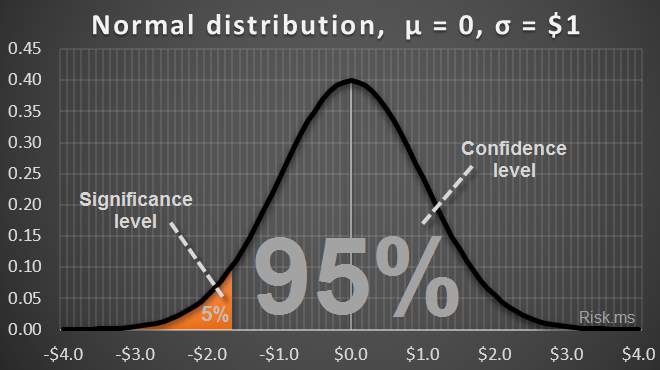
Pre-specified probability can be defined as the confidence level (1–α) or as the significance level (α):
- Confidence level (1–α, which is typically a large value, e.g. 95%) is the probability that the loss will be lower then VaR;
- Significance level (α, which is typically a small value, e.g. 5%) is the probability that the loss will be higher than VaR.
An example of VaR for normal-distributed profits&losses :
VaR estimation approaches
Historical-based approaches
The common feature of all the approaches within this set is their use of historical time series data in order to determine the parameters of the conditional distribution.
Non-parametric approach
The nonparametric approach uses historical data directly, without any assumptions about the distribution. The simplest and most prominent example of this approach is the historical simulation.
Parametric approach
The parametric approach implies a specific assumption about the distribution of asset returns. The most prominent example of this approach is the conditional normal (lognormal) distribution with time-varying volatility, where volatility is estimated from recent past data.
Hybrid approach
The hybrid historical approach is a combined approach of parametric and nonparametric methods.
Implied-Volatility-based approach
This approach uses current derivative prices and derivative pricing models to assign implied volatility (IV). The most prominent representative of these models is the use of IV obtained from the Black-Scholes option pricing model.