Excel: Black-Scholes-Merton Option Price and Greeks

Black-Scholes-Merton (or BSM) model is the most popular and widely-used option pricing model. Below, there is an example of the calculation of the BSM option price and option Greeks in Excel.

1. Black-Scholes Option Price in Excel without VBA

Download an example xlsx

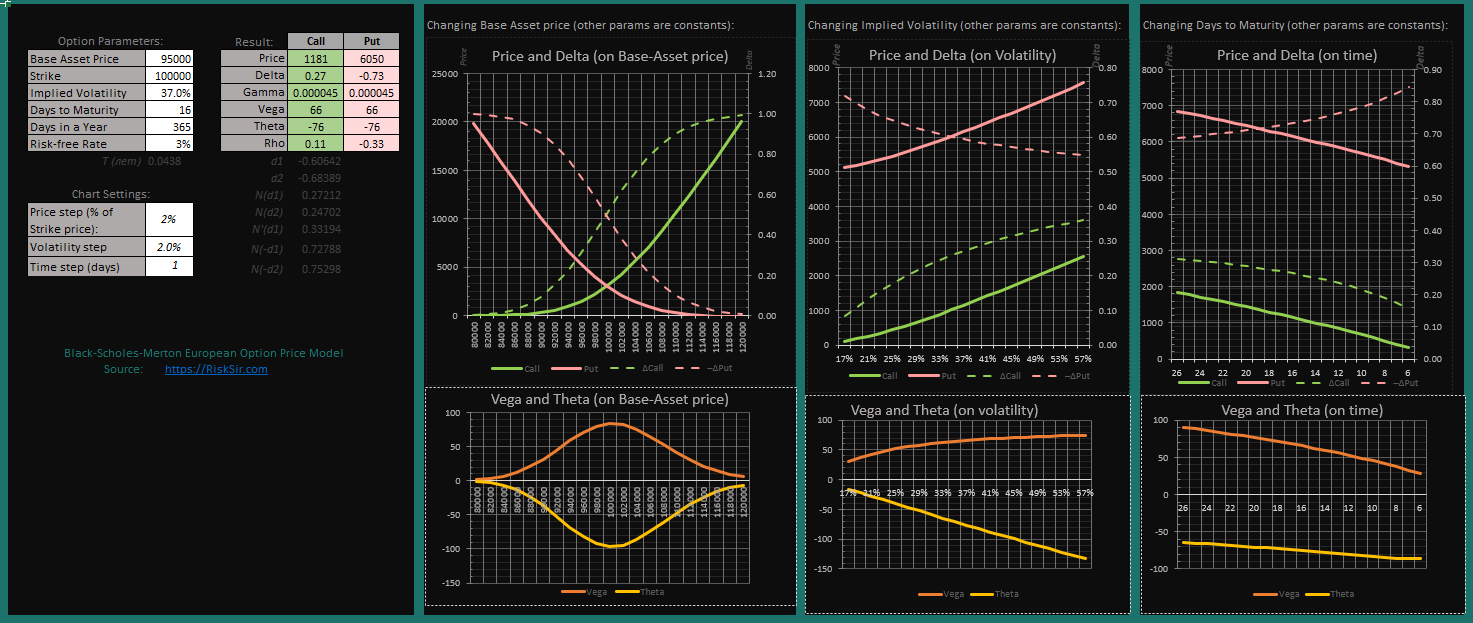
2. Black-Scholes Option Price in Excel with VBA

'-------------------------------------------------------------------------
' Source: risksir.com
' Description: Black-Scholes-Merton European Option Price Model
'-------------------------------------------------------------------------
'-------------------------------------------------------------------------
' S — Base Asset Price
' X — Strike
' d — Days to maturity (if 0 -> takes 0.3 days)
' y — Days in one year
' v — Implied volatility (if 0 -> takes 10^(-10))
' r — Risk-free rate
'-------------------------------------------------------------------------

' PRICE
Function OptionPrice(OptionType, S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If (OptionType = "Call" Or OptionType = "CALL") Then
    OptionPrice = S * Nd_1(S, X, d, y, v, r) - X * Nd_2(S, X, d, y, v, r) * Exp(-r * T)
ElseIf (OptionType = "Put" Or OptionType = "PUT") Then
    OptionPrice = X * N_d_2(S, X, d, y, v, r) * Exp(-r * T) - S * N_d_1(S, X, d, y, v, r)
ElseIf (OptionType = "BA") Then
    OptionPrice = S
End If
End Function

' DELTA
Function OptionDelta(OptionType, S, X, d, y, v, r)
If (OptionType = "Call" Or OptionType = "CALL") Then
    OptionDelta = Nd_1(S, X, d, y, v, r)
ElseIf (OptionType = "Put" Or OptionType = "PUT") Then
    OptionDelta = Nd_1(S, X, d, y, v, r) - 1
End If
End Function

' THETA
Function OptionTheta(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If v = 0 Then v = 10 ^ (-10)
    OptionTheta = -((S * v * N1d_1(S, X, d, y, v, r)) / (2 * (T ^ 0.5))) / y
End Function

' GAMMA
Function OptionGamma(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If v = 0 Then v = 10 ^ (-10)
OptionGamma = N1d_1(S, X, d, y, v, r) / (S * (v * (T ^ 0.5)))
End Function

' VEGA
Function OptionVega(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If v = 0 Then v = 10 ^ (-10)
OptionVega = (S * (T ^ 0.5) * N1d_1(S, X, d, y, v, r)) / 100
End Function

' RHO
Function OptionRho(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If v = 0 Then v = 10 ^ (-10)
OptionRho = X * T * Exp(-r * T) * Nd_2(S, X, d, y, v, r) / 10000
End Function



Function d_1(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
If v = 0 Then v = 10 ^ (-10)
d_1 = (Log(S / X) + (r + 0.5 * (v ^ 2)) * T) / (v * (T ^ 0.5))
End Function

Function d_2(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
d_2 = d_1(S, X, d, y, v, r) - v * (T ^ 0.5)
End Function

Function Nd_1(S, X, d, y, v, r)
Nd_1 = Application.NormSDist(d_1(S, X, d, y, v, r))
End Function

Function Nd_2(S, X, d, y, v, r)
Nd_2 = Application.NormSDist(d_2(S, X, d, y, v, r))
End Function

Function N_d_1(S, X, d, y, v, r)
N_d_1 = Application.NormSDist(-d_1(S, X, d, y, v, r))
End Function

Function N_d_2(S, X, d, y, v, r)
N_d_2 = Application.NormSDist(-d_2(S, X, d, y, v, r))
End Function

Function N1d_1(S, X, d, y, v, r)
If d > 0 Then
 T = d / y
 Else: T = 0.3 / y
End If
N1d_1 = 1 / (2 * Application.Pi()) ^ 0.5 * (Exp(-0.5 * d_1(S, X, d, y, v, r) ^ 2))
End Function

Download an example xlsm